고정 헤더 영역
상세 컨텐츠
본문
https://school.programmers.co.kr/learn/courses/30/lessons/87391
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr

처음 문제접근
문제에서 제시된 시뮬레이션대로
각 좌표를 돌면서
쿼리대로 수행했을 때
목표한 x,y지점에 가는지 판단
시간초과이유
n*m*query갯수
최악의 케이스를 고르면
10^9 * 10^9 *200000
그럼 어떻게 고쳐야할까?
구글링을 통해 알아낸 접근입니다.
1. 쿼리만 수행하도록 고쳐도
최대 200000으로 확 줄어든다.
2. 쿼리를 역으로 수행해서
모두 수행했을 때 x,y지점으로 들어가는지 판단한다.
3. x,y지점에 점이 모여있다고 생각하고,
점이 있는 구역을 사각형이라고 생각해보자.
그림설명

만약에 x,y가 0,0이라고 가정해보고
문제를 설명해보겠습니다.
x,y 지점에는 한 개의 점만 존재합니다.
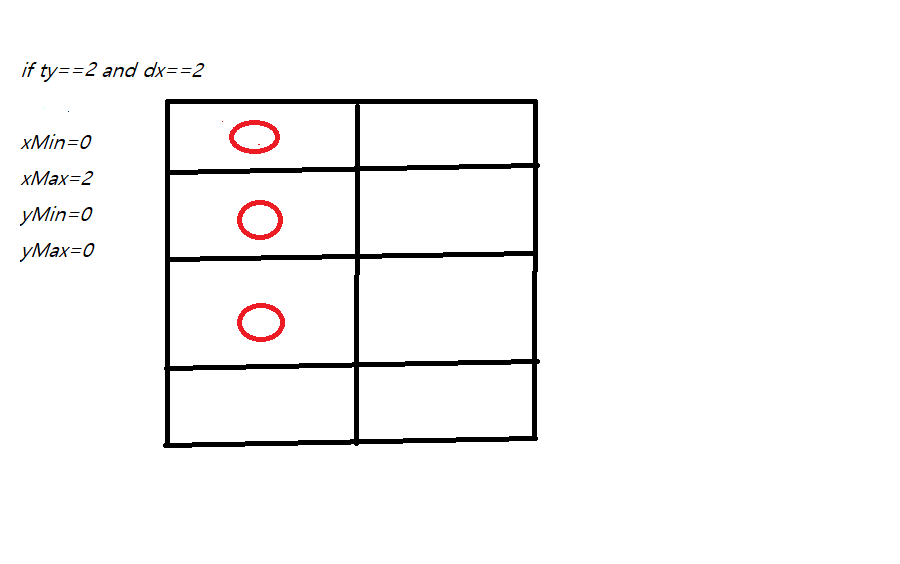
query ty==2 이고 dx==2인 경우에는
행이 줄어드는 경우입니다.
어떤 좌표에서 이렇게 수행할 때 0,0이 될까 추적하면
위의 그림처럼 그릴 수 있습니다.
이를 다시 생각해보면
xMax가 늘어났고
이런 식으로 x,y중 최대 최소를 구해서
"점이 있는 직사각형의 넓이"를 구한다고 생각할 수 있습니다.
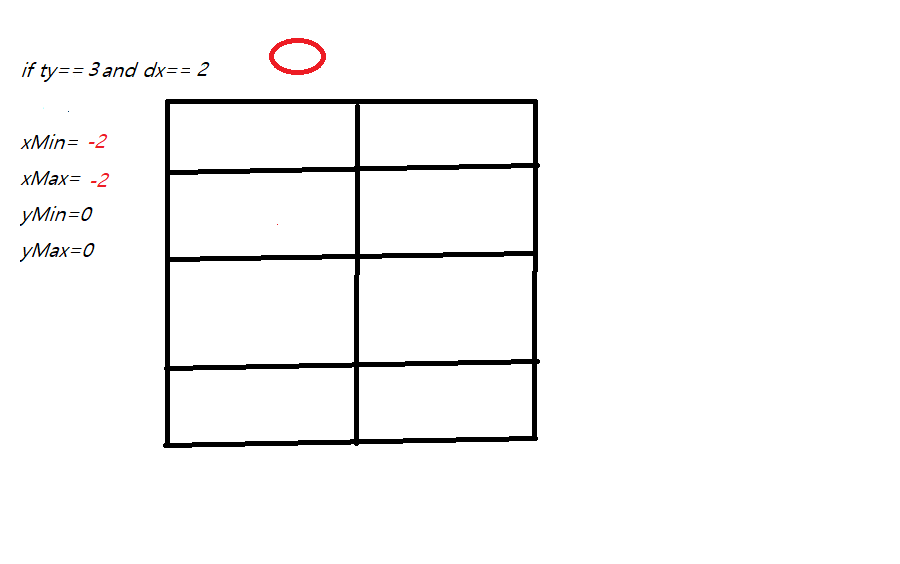
만약에 범위를 벗어나는 케이스가 있다면
답은 0이 될 수 밖에 없습니다.
x,y가 0,0인 상황에서
ty==3 이 떠서 공의 최댓값이 범위를 벗어나버렸습니다.
역으로 연산했더니 공이 범위 밖의 것이 나왔다는 건
이전에 뭘했던지 간에 결국 범위안에 공이 없다는 의미이므로
0을 리턴해주면 됩니다.

여기서 주의할 점은
Min,Max도 함꼐 움직일 수 있다는 점.
x,y가 0,0일때 ty==2일때는 xMin이 고정되어있지만
1,0 인 케이스에서는 xMin도 함께 이동합니다.
처음에 코드로만 봤을 때는 이게 무슨 말인지 이해가 되지 않았는데
직접 그림을 그려보니간 이해가 되었습니다.
행을 하나만큼 감소해서 1,0이 되는 좌표를 그려보면
딱 저 하나의 케이스만 나옵니다.
그러니 우리가 점이 있는 사각형을 구할 때
xMin값도 함께 움직여야합니다.
이런 식으로 다른 케이스에서도 그림을 그려가면서
"이럴 때는 어떻게 되는가?"염두하시면서 코드를 짜면 도움이 되실 겁니다.
코드
def solution(n, m, x, y, queries):
answer = 0
# 공이 한번에 움직인다고 생각한다
# 공의 범위를 사각형으로 두고 생각해보자
# 역으로 생각한다
queries.reverse()
xMin, xMax, yMin, yMax = x, x, y, y
# print(queries)
for ty, dx in queries:
# 원래 열감소니깐 여기서는 열증가로 계산
if ty == 0:
yMax += dx
if yMax >= m:
yMax = m - 1
if yMin != 0:
yMin += dx
# 원래는 열증가니깐 여기서는 열감소로 계산
elif ty == 1:
yMin -= dx
if yMin < 0:
yMin = 0
if yMax != m - 1:
yMax -= dx
# 원래는 행감소니깐 여기서는 행증가로 계산
elif ty == 2:
xMax += dx
if xMax >= n:
xMax = n - 1
if xMin != 0:
xMin += dx
# 원래는 행 증가니깐 여기서는 행감소로 계산
elif ty == 3:
xMin -= dx
if xMin - dx < 0:
xMin = 0
if xMax != n - 1:
xMax -= dx
# 범위를 벗어나는 케이스가 생긴다면 공이 없다
# print(xMin,xMax,yMin,yMax)
if xMin > n or xMax < 0 or yMin > m or yMax < 0:
return 0
else:
answer = (xMax - xMin + 1) * (yMax - yMin + 1)
return answer
'알고리즘 공부' 카테고리의 다른 글
| [프로그래머스Lv.3] 기둥과 보 설치(파이썬) (1) | 2023.03.01 |
|---|---|
| [프로그래머스Lv.3] 미로탈출 명령어(파이썬) (0) | 2023.02.27 |
| [프로그래머스Lv.3] 등산코스정하기(파이썬) (0) | 2023.02.20 |
| [프로그래머스Lv.3] 퍼즐조각 채우기(파이썬) (0) | 2023.02.17 |
| [프로그래머스] 주식가격(파이썬) (3) | 2023.01.13 |






댓글 영역