고정 헤더 영역
상세 컨텐츠
본문
컴퓨터는 0과 1만 이해한다고 흔히 알고 있습니다.
왜 컴퓨터는 굳이 2진수로 계산을 하는 걸까요?
그리고 프로그래머입장에서 왜 2진수 계산을 알아야할까요??
컴퓨터가 2진수를 사용하는 이유
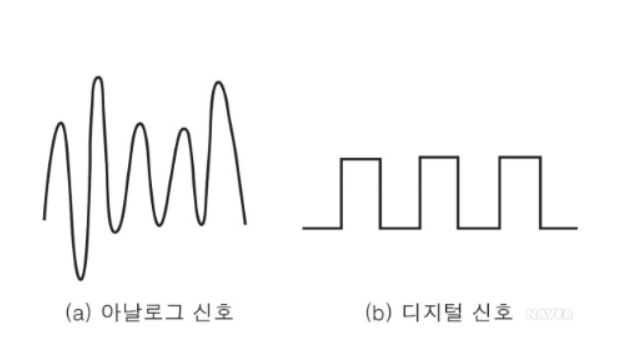
전자기기들은 디지털신호를 활용해서 정보를 처리합니다.
디지털신호는 아날로그 신호 대비
간결하고 노이즈가 없습니다.

컴퓨터내부를 보면 수 많은 전자부품들이 들어가있습니다.
이 수 많은 부품들을 어떻게 효율적으로 제어하면서 연산을 수행할까요?

바로 다음과 같은 '논리회로'로 컴퓨터 내부를 구성하는 방법이 있습니다.
논리회로는 0과 1의 값으로 논리연산한 결과를 내보내기 때문에
아날로그회로 대비 쉽게 결과를 예측할 수 있고
정보표현이 간결합니다.
그리고 0.33222 등등의 애매한 숫자없이(즉, 노이즈가 없음) 동작하기 때문에
논리적으로 수행했을 때 결과가 모두 동일하여 안정성을 확보할 수 있습니다.
여기서 왜 컴퓨터가 2진수를 써야하는지로 이어지는데요
논리회로를 사용할 때
입력값으로 0011 이런 식으로 입력을 하여
각 회로에 어떻게 동작하는지 결정하기 때문에
컴퓨터 내부의 동작을 작동하고 이해하기 위해서는
이진수를 사용해야합니다.

그래서 컴퓨터 명령어는
다음과 같이 2진수 숫자로 이뤄진 폼으로 구성이 되어있습니다.
그래서 컴퓨터 명령어가 각각 어떤 구성인지 이해하기 위해서는
이 명령어 구조를 제대로 파악해야겠죠
프로그래머가 2진수 계산을 알아야하는 이유
"그건 컴퓨터가 할 일이지, 프로그래머가 할 일은 아니지 않나?"
혹자들은 이런 의문을 제기합니다.
프로그래머는 코드만 잘 짜면 되는데
왜 사용하기 불편한 2진수 계산을 알아야할까요?
하드웨어제어
for (int i = 8; i >= 1; i--) {
if (X & 0x80) {
HAL_GPIO_WritePin(FND_DIO_GPIO_Port, FND_DIO_Pin, HIGH);
} else {
HAL_GPIO_WritePin(FND_DIO_GPIO_Port, FND_DIO_Pin, LOW);
}
X <<= 1;
HAL_GPIO_WritePin(FND_SCLK_GPIO_Port, FND_SCLK_Pin, LOW);
HAL_GPIO_WritePin(FND_SCLK_GPIO_Port, FND_SCLK_Pin, HIGH);
}제가 했던 프로젝트에서
FND묘듈(7세그먼트)를 동작과 관련한 코드입니다.
코트에서 X<<=1은 X의 값을 1만큼 shift시켰다는 의미입니다.
X의 값이 11100000이라고 가정하면
1110000
1100000
1000000
0000000(이후 계속 0000000)
이렇게 X값이 shift됩니다.
if문에서는 X의 값과 0x80(10000000)의 값을 &연산시킵니다.
그래서 계산결과가 1이 되는 경우에는 FND port에 High를 보내 동작시키고
그렇지 않다면 Low를 해서 동작하지 않습니다.
케이스 관리

바둑판은 경우의 수가 정말 많습니다.
해당 그림은 19*19이기 때문에
돌을 배치하는 모든 케이스를 다 고려해보면
(2^19)^19
이라는 어마어마한 경우의 수가 나옵니다.
이렇게 많은 숫자를 관리할 때 어떻게 관리할까요?
돌이 넣을 때를 1,안 넣을 때를 0으로 두면
19자리 이진수가 19줄있는 데이터로 구할 수 있습니다.
이 경우도 무지 복잡하긴 하지만
2진수로 두어 데이터관리를 조금이나마 효율적으로 할 수 있습니다.
네트워크 IP주소
# IP 주소와 서브넷 마스크를 이진수로 변환
ip_address = "192.168.1.100"
subnet_mask = "255.255.255.0"
ip_binary = '.'.join(format(int(x), '08b') for x in ip_address.split('.'))
subnet_mask_binary = '.'.join(format(int(x), '08b') for x in subnet_mask.split('.'))
print("IP 주소 (이진수):", ip_binary)
print("서브넷 마스크 (이진수):", subnet_mask_binary)
# 서브넷 주소 계산
network_address = ''.join([str(int(ip_binary[i]) & int(subnet_mask_binary[i])) for i in range(32)])
network_address = '.'.join([network_address[i:i+8] for i in range(0, 32, 8)])
print("네트워크 주소 (이진수):", network_address)위의 코드는 IP주소와 서브넷 마스크를 이진수로 변환한 후
네트워크 주소를 계산한 예시입니다.
다음과 같은 계산과정이 있기 때문에
네트워크 프로그래머들도 이진수 계산방법을 알아야합니다.
2진수 연산에 대해 알아보자
뎃셈,뺄셈


덧셈,뺄셈은 사칙연산과 같이
각 자리수를 더하고 빼는 식으로 계산할 수 있습니다.
(참고로, 컴퓨터에서는 비트가 제한이 되는 경우가 있어서
만약에 위의 덧셈케이스에서 비트가 제한될 경우
오버플로우가 되어 0000으로 출력이 됩니다.)
AND

and(&)연산의 경우,
자리수를 비교하고 두 자리 모두 1이면 1.
그 외의 경우는 모두 0입니다.
특정 자리수의 값을 구할 때
&연산을 통해 활용할 수 있는데,
그림에서는 4번째 자리가 1인 경우에는 1이라는 걸 이용할 수 있는데
if (X&1000){
//특정 동작
}이렇게되면 X가 8이상일 경우에는
if문의 조건을 만족하는 형태가 됩니다.
OR

or(||)연산은 두 숫자에서
하나만 1이어도 1의 결과가 출력되는 연산입니다.
XOR

XOR(^)연산은 두 비트가 서로 다를 때 1을 나타냅니다.
NOT

NOT(~)연산은
비트 자리수를 0->1/1->0으로 바꾸는 연산을 합니다.
Shift


Shift연산(<<,>>)은
자릿수를 왼쪽,오른쪽으로 이동시키는 연산을 의미합니다.
위 그림은 1만큼 shift한 케이스를 다루었으며
<< x는 왼쪽으로 x만큼 이동하며
2^x만큼 곱한 것과 같은 효과를 줍니다.
>>x는 오른쪽으로 x만큼 이동하며
2^x만큼 나눈 것과 같은 효과를 줍니다.
for (int i = 8; i >= 1; i--) {
if (X & 0x80) {
HAL_GPIO_WritePin(FND_DIO_GPIO_Port, FND_DIO_Pin, HIGH);
} else {
HAL_GPIO_WritePin(FND_DIO_GPIO_Port, FND_DIO_Pin, LOW);
}
X <<= 1;
HAL_GPIO_WritePin(FND_SCLK_GPIO_Port, FND_SCLK_Pin, LOW);
HAL_GPIO_WritePin(FND_SCLK_GPIO_Port, FND_SCLK_Pin, HIGH);
}아까 위에서 봤던 코드를 다시 가져왔습니다.
for문을 돌면서 X를 1만큼 왼쪽으로 shift해줍니다.
그래서 X의 자릿수가 0x80과 &연산을 하여
1이 되었을 때에 FND에 HIGH를 인가하는 코드입니다.
2의 보수(complement)

컴퓨터로 각 비트에 숫자를 입력하여
2진수의 숫자를 저장한다는 것은 알았습니다.
그렇다면 음수는 어떻게 나타낼까요?
이런 음수를 표현하기 위해
'보수'라는 개념을 활용해
2의 보수를 만듭니다.
보수란 두 수의 합이 진법의 N밑 수가 되게 하는 수를 말합니다.
예를들어
10진수에서 4의 보수는 6.
10진수에서 2의 보수는 8
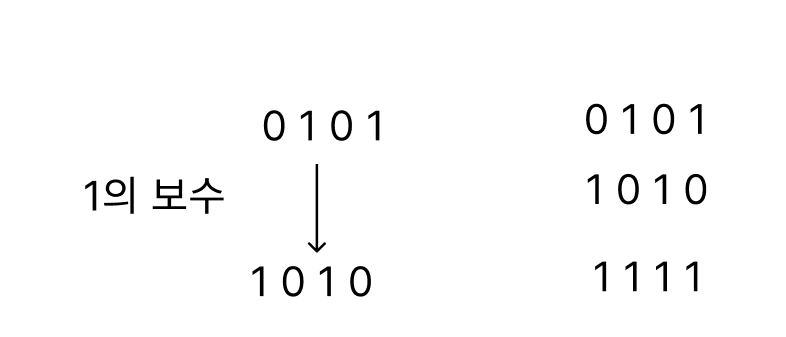
0101의 2의 보수를 만드는 과정을 보겠습니다.
먼저, 2진수에서의 1의 보수를 먼저 구합니다.
각 자리수를 반전시킨 것이 1의 보수입니다.

2의 보수는 1의 보수에 1을 더한 값입니다.
위에서 구한 1의 보수에 1을 더하면
0101의 2의 보수는 1011입니다.
signed Bit

컴퓨터에서는 맨 앞의 숫자를 부호를 표현하는
sigined Bit로 둡니다.
0이면 양수, 1이면 음수로 인식합니다.
위의 경우를 보면
1011은
->-8+3+1=-5로 인식합니다.
정수 범위

해당 표는 32비트 운영체제에서
int값의 범위입니다.
왜 다음과 같은 범위가 주어질까요?

32개의 비트를 모두 1로 두면
십진수로 다음의 값이 주어짐을 알 수 있습니다.
부호가 없는 unsigned의 경우에는 0~4,294,967,295까지 모두 표현할 수 있습니다.
하지만 부호가 있는 signed의 경우, 맨 앞자리는 부호로 표시하기 때문에
그 범위가 -2,147,483,647~2,147,483,647로 범위가 변경됩니다.
'CS지식 학습' 카테고리의 다른 글
| CPU Clock은 무엇이고 어떻게 활용될까? (0) | 2023.10.12 |
|---|---|
| 메모리와 명령어의 상호작용, 왜 알아야할까?? (1) | 2023.10.10 |
| 레지스터, 왜 알아야하고 어떻게 동작할까? (0) | 2023.10.05 |
| (어그로 아님) int자료형은 언제나 4바이트가 아니다 (0) | 2023.09.24 |
| Call by value vs Call by reference??? (C언어 고찰) (0) | 2023.09.23 |





댓글 영역